Wooden Bridge Building
|
Did you lose your worksheet?!
Download the worksheet here: |
| ||||||
Project parameters:
- You will be supplied with 1 pine 8ft 2x4 (cut into 1/2" x 1/2” strips)
- The wood may be joined with glue and staples
- One piece of sheet metal to use as a “driving surface” or reinforced struts
- No other materials may be used
Challenge:
- Your bridge will have to cross a 34 inch gap and withstand down forces and weight. Your bridge must be 36 inches long. 1 inch of each side will rest on the holding jig.
- A weight bucket will be placed on top of your bridge and filled with gravel/rocks until it reaches a failing weight
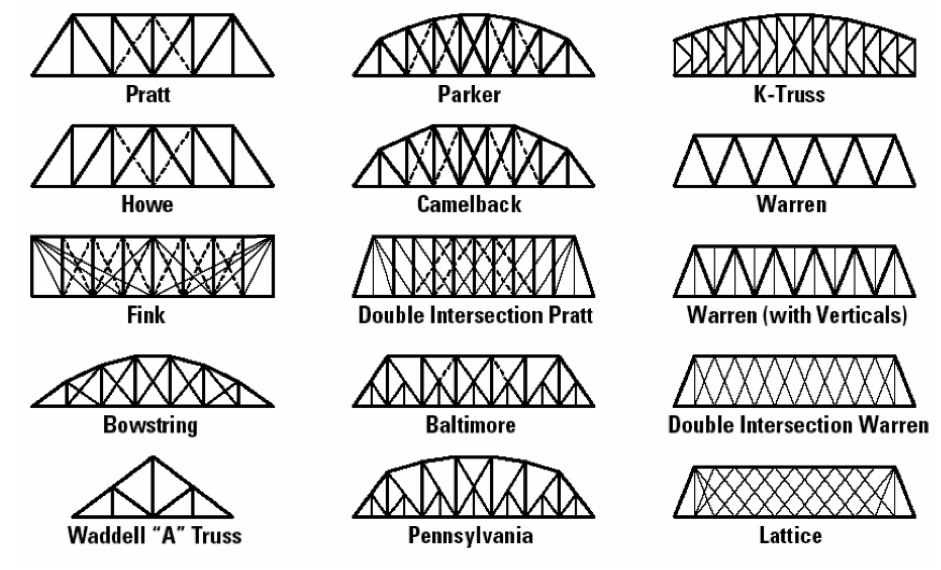
- You may build any style bridge but must only use the supplied materials
- Wood frame thickness must be no thicker than 1/2”x1/2” square pieces
- A toy car must be pulled on a string/rope across the driving surface of your bridge from one side to the other
Groups:
Teams are to be no more than 4 people (minimum 2). Each group member should have a specific role during the project but all should be working everyday and helping each other.
Planning:
The design phase is a very important process with this project as there will be no extra materials given. Detailed plans of your bridge including different angles of view and measurements must be included with your final project team booklet. We will go over in class what a proper scale drawing looks like.
The planning booklet makes up 40% of your grade. The planning booklet needs to be handed in prior to material being given out
Grading:
Planning booklet: 40%
Design and build quality: 50%
Competition marks: 10%
Design Drawings
A full size scale drawing(s) is required prior to cutting out materials. It should be drawn in a 2nd Orthographic style with each view labeled. Paper can be taped together to draw it full size.
Any sketches and original drawings should be included as part of a final ‘portfolio’ for this project to show your research and ideas.
Documenting your project from start to finish using both photos is required and will get you marks as part of the planning booklet (40%!!!) A word document or PDF can be emailed to the teacher with the progression of photos and a sentence explaining what is happening in the photos. An example portfolio write up can be found on Mr Holbrook’s website for the Arcade Cabinet @ http://holbrooktech.weebly.com/pi-arcade-101.html
If you choose also create a video please upload it to YouTube as “unlisted” and share the link via email with the teacher.
Evaluation
Questions for the individual groups:
1.How did you come up with the initial design for your bridge?
2.Did your design change as you built your bridge?
3.Which geometric shapes did you use in your bridge? Why?
4.How does the strength of the bridge compare to the weight of the bridge?
5.Would you make any changes in the design of your bridge?
Questions for the whole class:
1. Which bridge was the longest? Tallest? Strongest? Heaviest? Why?
2. What materials do you envision being used in future bridges?
3. How can computers help design bridges?
Timeline:
- Research and design – 3-4 classes
- Build time 15 classes
Learning Expectations:
•Recognize design components which occur regularly.
•Understand principles of good design.
•Analyze how structural components react to stresses.
•Compare the strengths of different components of a structure.
•Create procedures for constructing and testing components of a structure.
•Use some of the elements and principles of design to build objects.
•Examine experiences with various structures in the home and in the school.
•Explore the benefits and limitations of structures.
•Investigate the technical, social, and cultural implications of design and construction of objects.
•Promote both intuitive, imaginative thought and the ability to evaluate ideas, processes, experiences and objects in meaningful contexts.
•Develop ways to evaluate creative processes and projects.
•Use metaphoric and analogical thinking to create insights and build understanding about structures.
•Determine that real-life problems often have more than one solution.
•Discover relationships and patterns.
•Imagine and manipulate objects and ideas.
•Provide arguments related to principles and to evidence for ideas and choices expressed.
•Discuss why structures are constructed.
•Demonstrate understanding of the concepts of perimeter, area, volume, angle measure, capacity, weight and mass, and of any related formulas; demonstrate an understanding of rates and other derived and indirect measurements;
•In order to develop algebraic thinking through an understanding of patterns and functions, the mathematics curriculum must include problems which require students to describe, extend, analyze, and create a wide variety of patterns and functions using appropriate materials and representations such as tables, graphs, and mathematical notation. represent situations with tables, graphs, verbal rules, and equations and describe the interrelationships of the representations; identify patterns and functions from statistical data
•In order to develop an understanding of statistics and probability, the mathematics curriculum must include problems which require students to collect, organize, represent, and interpret data; make inferences and predictions; present and evaluate inferences and predictions; present and evaluate arguments based on data analysis; and model situations to determine theoretical and experimental probabilities.
•Collect, organize, and describe data in order to make conjectures; formulate and test hypotheses, draw conclusions, and make convincing arguments that are based on data analysis
•By incorporating prior knowledge with the process of observation, a better understanding of one's environment may develop.
•Scientific investigation is enhanced through the use of technology.
•The reading and interpretation of measuring instruments are (is) necessary in determining length, volume, weight, elapsed time, rates, and temperature.
•Safety procedures are introduced prior to and practiced during all data collection.
•An equation containing a variable may be true for just one value of the variable.
•In formation is organized into simple tables and graphs to identify relationships.
•Mathematical statements can be used to describe the magnitudes of change one quantity has on another.
•The graphic display of numbers may help to show patterns such as trends, varying rates of change, gaps,or clusters.
•Written, verbal presentations can be used to interpret and expand more abstract mathematical concepts.
•Prior knowledge provides a foundation for new learning experiences.
•Human beings learn complicated concepts from others through various methods of communcation.
•Models are often used to represent concepts of various magnitudes.
•The usefulness of a graph or drawing is determined by the scale utilized.
•Specialized structures perform specific functions.
•All objects in the universe are affected by the gravitational forces.
•Any change or error in design may affect function.
•Design usually requires taking constraints into account.
•Estimation of probability can be based on data from similar conditions in the past or what is known about current situations.
•An investigator's credibility depends upon accurate record keeping, openness, and replication.
•People who engage in design and technology use scientific knowledge to solve practical problems
•Observe and compare the shapes found in some natural and some human-constructed objects.
Resources:
http://mfranzen.ca/pages/cor/tij1o1_u2.html
http://www.bridgebuilder-game.com/
Bridge Builder @ Crazy Games
https://www.crazygames.com/game/bridge-builder
download the game from here if on school computer (PC only). 1) unzip 2) drag to your documents folder 3) play!
https://www.dropbox.com/sh/ljgan5bfqjqoic8/AACdHwoXXN3X1dclukK85nZIa?dl=0
Example bridges: